Algèbre

L'importance de Maxima comme logiciel de calcul formel appairait clairement quand nous voyons avec quelle facilité le logiciel va effectuer des calculs algébriques. Voici un exemple de développement d'un polynôme :

(C1) (x+3*y+x^2*y)^3;

$\text{\texttt{{\red (D1) {\black }}}} \left( x^2 y + 3 y + x \right)^3$

(C2) expand(%)

$\text{\texttt{{\red (D2) {\black }}}} x^6 y^3 + 9 x^4 y^3 + 27 x^2 y^3 + 27 y^3 + 3 x^5 y^2 + 18 x^3 y^2 + 27 x y^2 + 3 x^4 y + 9 x^2 y + x^3$

Supposons maintenant que nous voulons remplacer $x$ par la valeur $\frac{5}{z}$ dans l'expression précédente :

maxima] d2,x=5/z;

$\text{\texttt{{\red (D4) {\black }}}} \frac{135 y^2}{z} + \frac{675 y^3}{z^2} +... ...4} + \frac{1875 y}{z^4} + \frac{9375 y^2}{z^5} + \frac{15625 y^3}{z^6} + 27 y^3$

La fonction RATSIMP de Maxima réduit l'expression au même dénominateur :

maxima] ratsimp(%)

$\text{\texttt{{\red (D5) {\black }}}} \frac{27 y^3 z^6 + 135 y^2 z^5 + \left( 6... ...ight) z^3 + \left( 5625 y^3 + 1875 y \right) z^2 + 9375 y^2 z + 15625 y^3}{z^6}$

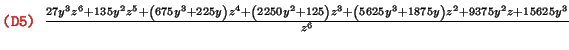
Les expressions peuvent être factorisées :

maxima] factor(%)

$\text{\texttt{{\red (D6) {\black }}}} \frac{\left( 3 y z^2 + 5 z + 25 y \right)^3}{z^6}$

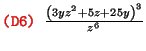
Maxima peut trouver les valeurs exactes des solutions de systèmes d'équations algébriques, même dans des cas non linéaires. Dans l'exemple suivant, on résout trois équations dont les inconnues sont $a$, $b$ et $c$ :

maxima] a+b*c=1;

$\text{\texttt{{\red (D7) {\black }}}} b c + a = 1$

(C8) b-a*c=0;

$\text{\texttt{{\red (D8) {\black }}}} b - a c = 0$

(C9) a+b=5;

$\text{\texttt{{\red (D9) {\black }}}} b + a = 5$

(C10) solve([d7,d8,d9],[a,b,c]);

$\text{\texttt{{\red (D10) {\black }}}} \left[ \left[ a = \frac{25 \sqrt{79} i +... ...{79} i - 5}{\sqrt{79} i - 11}, c = - \frac{\sqrt{79} i - 1}{10} \right] \right]$

Remarquez que la sortie consiste en une " liste ", c'est à dire en une expression comprise entre deux crochets [ ... ], qui contient elle-même deux listes. Chacune de ces dernières contient une solution au système d'équations.

Les formules trigonométriques se manipulent aisément avec Maxima. La fonction TRIGEXPAND utilise la formule de la somme afin de simplifier au maximum l'argument de chacune des fonctions trigonométriques utilisées :

(C1) sin(u+v)*cos(u)^3;

$\text{\texttt{{\red (D1) {\black }}}} \cos^3 u \sin \left( v + u \right)$

(C2) trigexpand(%)

$\text{\texttt{{\red (D2) {\black }}}} \cos^3 u \left( \cos u \sin v + \sin u \cos v \right)$

Inversement, la fonction TRIGREDUCE transforme une expression trigonométrique en une somme de termes dont chacun ne comporte qu'une seule fois la fonction sinus ou la fonction cosinus :

maxima] trigreduce(d1);

$\text{\texttt{{\red (D3) {\black }}}} \frac{\sin \left( v + 4 u \right) + \sin \left( v - 2 u \right)}{8} + \frac{3 \sin \left( v + 2 u \right) + 3 \sin v}{8}$

Les fonctions REALPART et IMAGPART renvoient respectivement la partie réelle et la partie imaginaire d'un nombre complexe :

maxima] w:3+k*%i;

$\text{\texttt{{\red (D4) {\black }}}} i k + 3$

(C5) w^2*%e^w;

$\text{\texttt{{\red (D5) {\black }}}} \left( i k + 3 \right)^2 e^{i k + 3}$

(C6) realpart(%)

$\text{\texttt{{\red (D6) {\black }}}} e^3 \left( 9 - k^2 \right) \cos k - 6 e^3 k \sin k$

(C7) imagpart(D5);

$\text{\texttt{{\red (D7) {\black }}}} e^3 \left( 9 - k^2 \right) \sin k + 6 e^3 k \cos k$